MATEMATICAS - TRIGONOMETRIA

TRIGONOMETRIA

La trigonometría es una rama de las matemáticas de antiguo origen, cuyo significado etimológico es ("la medición de los triángulos"). Se deriva del vocablo ← griego τριγωνο <trigōno> "triángulo" + μετρον <metron> "medida"[1] ,
La trigonometría en principio es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de las razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos. En términos generales, la trigonometría es el estudio de las funciones seno, coseno, tangente, cotangente, secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía.

Razones trigonométricas

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo $alpha ,$ , correspondiente al vértice A, situado en el centro de la circunferencia.

El seno (abreviado como sen, o sin por llamarse "sinus" en latín) es la razón entre el cateto opuesto y la hipotenusa,

$operatorname{sen}(alpha)= frac{a}{c}$

El coseno (abreviado como cos) es la razón entre el cateto adyacente y la hipotenusa,

$cos(alpha)= frac{b}{c}$

La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto y el adyacente,

$tan(alpha)= frac{a}{b}$

Es el cociente del seno entre el coseno.

Razones Trigonométricas Recíprocas

Se definen la cosecante, la secante y la cotangente, como las razones recíprocas al seno, coseno y tangente, del siguiente modo:

secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:

$sec (alpha) = frac{1}{cos (alpha)} = frac{c}{b}$

cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:

$csc (alpha) = frac{1}{operatorname{sen} (alpha)} = frac{c}{a}$

cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:

$cot (alpha) = frac{1}{tan (alpha)} = frac{b}{a}$

Funciones trigonométricas inversas

En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual al radio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones inversas se denominan con el prefijo arco, así si:

$y= operatorname{sen}(x) ,$

y es igual al seno de x, la función inversa:

$x = operatorname{arcsen}(y) ,$

x es el arco cuyo seno vale y, o también x es el arcoseno de y.

si:

$y= cos(x) ,$

y es igual al coseno de x, la función inversa:

$x = arccos(y) ,$

x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.

si:

$y= tan(x) ,$

y es igual al tangente de x, la función inversa:

$x = arctan(y) ,$

x es el arco cuyo tangente vale y, ó x es igual al arcotangente de y.

Valor de las funciones trigonométricas

A continuación algunos valores de las funciones que es conveniente recordar:

Radián	Ángulo	sen	cos	tan	csc	sec	ctg
$0 ;$	$0^o ,$	$frac{sqrt{0}}{2}=0$	$frac{sqrt{4}}{2}=1$	$0 ,$	$infty$	$1 ,$	$infty$
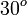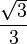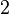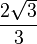$frac{pi}{6}$	$30^o ,$	$frac{sqrt{1}}{2}=frac{1}{2}$	$frac{sqrt{3}}{2}$	$frac{sqrt{3}}{3}$	$2 ,$	$frac{2sqrt{3}}{3}$	$sqrt{3}$
$frac{pi}{4}$	$45^o ,$	$frac{sqrt{2}}{2}$	$frac{sqrt{2}}{2}$	$1 ,$	$sqrt{2}$	$sqrt{2}$	$1 ,$
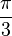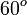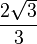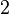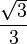$frac{pi}{3}$	$60^o ,$	$frac{sqrt{3}}{2}$	$frac{sqrt{1}}{2}=frac{1}{2}$	$sqrt{3}$	$frac{2sqrt{3}}{3}$	$2 ,$	$frac{sqrt{3}}{3}$
$frac{pi}{2}$	$90^o ,$	$frac{sqrt{4}}{2}=1$	$frac{sqrt{0}}{2}=0$	$infty$	$1 ,$	$infty$	$0 ,$

Para el calculo del valor de las funciones trigonométricas se confeccionaron tablas trigonométricas. La primera de estas tablas fue desarrollada por Johann Müller Regiomontano en 1467, que nos permiten, conocido un ángulo, calcular los valores de sus funciones trigonométricas. En la actualidad dado el desarrollo de la informática, en prácticamente todos los lenguajes de programación existen librerías de funciones que realizan estos cálculos, incorporadas incluso en calculadoras electrónicas de bolsillo, por lo que el empleo actual de las tablas resulta obsoleto.

SENTIDO DE LAS FUNCIONES TRIGONOMETRICAS

Dados los ejes de coordenadas cartesianas xy, de centro O, y un círculo con centro en O y radio 1; el punto de corte de la circunferencia con el lado positivo de las x, lo señalamos como punto B.

La recta r, que pasa por O y forma un ángulo a sobre el eje de las x, corta a la circunferencia en el punto C, la vertical que pasa por C, corta al eje x en A, la vertical que pasa por B corta a la recta r en el punto D.

Por semejanza de triángulos:

$frac{; overline{AC} ;}{overline{OA}} = frac{; overline{BD} ;}{overline{OB}}$

La distancia $overline{OB}$ , es el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:

$operatorname{sen}(a)= overline{AC} ,$

$cos(a)= overline{OA} ,$

$tan(a)= overline{BD} ,$

tenemos:

$frac{operatorname{sen}(a)}{ cos(a)} = frac{tan(a)}{1}$

La tangente es la relación del seno entre el coseno, según la definición ya expuesta.

Primer cuadrante

Partiendo de esta representación geométrica de las funciones trigonométricas, podemos ver las variaciones de las funciones a medida que aumenta el ángulo a.

Para a = 0, tenemos que A, C, y D coinciden en B, por tanto:

$operatorname{sen}(0)= 0 ,$

$cos(0)= 1 ,$

$tan(0)= 0 ,$

Si aumentamos progresivamente el valor de a, las distancias AC y BD aumentaran progresivamente, mientras que OA disminuirá, percatarse que OA y AC están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero BD no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por B, en el momento en el que el ángulo a sea 0,5 $π$ rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia BD será infinita, la tangente toma valor infinito cuando a= 0,5 $π$ rad, el seno vale 1 y el coseno 0.

Segundo cuadrante

Cuando el ángulo a supera el ángulo recto, el valor del seno empieza a disminuir según el segmento AC, el coseno aumenta según el segmento OA, pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.

La tangente para un ángulo a inferior a 0,5 $π$ rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por B no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los 0,5 $π$ rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por B en un punto B real, en el lado negativo de las y, la tangente por tanto toma valor negativo, y su valor absoluto disminuye a medida que el ángulo a aumenta progresivamente hasta los $π$ rad.

Resumiendo: en el segundo cuadrante el seno de a, disminuye progresivamente su valor desde 1, que toma para a= 0,5 $π$ rad, hasta que valga 0, para a= $π$ rad, el coseno, toma valor negativo y su valor varia desde 0 para a= 0,5 $π$ rad, hasta –1, para a= $π$ rad.

La tangente conserva la relación:

$tan(a) = frac{operatorname{sen}(a)} {cos(a)}$

incluyendo el signo de estos valores.

Tercer cuadrante

En el tercer cuadrante, comprendido entre los valores del ángulo a de $π$ rad a 1,5 $π$ rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para $π$ rad:

$operatorname{sen}( pi ) = 0 ,$

$cos( pi ) = -1 ,$

$tan( pi ) = 0 ,$

Cuando el ángulo a aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.

A medida que el ángulo crece el punto A se acerca a O, y el segmento OA, el coseno se hace más pequeño en el lado negativo de las x, el punto C, intersección de la circunferencia y la vertical que pasa por A, se aleja del eje de las x, en el sentido negativo de las y, el seno, y el punto D, intersección de la prolongación de la recta r y la vertical que pasa por B, se aleja del eje las x en el sentido positivo de las y, la tangente.

Cuando el ángulo a alcance 1,5 $π$ rad, el punto A coincide con O y el coseno valdrá cero, el segmento OC será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por B serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.

El seno el coseno y la tangente siguen conservando la misma relación, tanto en valores como en signo, nótese que cuando el coseno vale cero, la tangente se hace infinito.

Cuarto cuadrante

En el cuarto cuadrante, que comprende los valores del ángulo a entre 1,5 $π$ rad y 2 $π$ rad, las variables trigonométricas varían desde los valores que toman para 1,5 $π$ rad:

$operatorname{sen}(1,5 , pi ) = -1 ,$

$cos(1,5 , pi ) = 0 ,$

$tan(1,5 , pi ) = infty ,$

hasta los que toman para 2 $π$ rad pasando al primer cuadrante, completando una rotación:

$operatorname{sen}(2 , pi ) = sin(0) = 0 ,$

$cos(2 , pi ) = cos(0) = 1 ,$

$tan(2 , pi ) = tan(0) = 0 ,$

como puede verse a medida que el ángulo a, también aumenta el coseno en el lado positivo de las x, el seno disminuye en el lado negativo de las y, y la tangente también disminuye en el lado negativo de las y.

Cuando a, vale 2 $π$ o 0 $π$ al completar una rotación completa los puntos A, B y C, coinciden en D, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.

IDENTIDADES TRIGONOMETRICAS

Una identidad es una igualdad en que se cumple para todos los valores permisibles de la variable. En trigonometría existen cinco identidades fundamentales :

Recíprocas :

s e n U * c s c U = 1

c o s U * s e c U = 1

t a n U * c o t U = 1

De división:

t a n U = s e n U / c o s U

Como en el triángulo rectángulo se cumple que $a 2 + b 2 = c 2$ , de la figura anterior se tiene que sen α = a, cos α = b, c = 1; entonces para todo ángulo &alpha, se cumple la identidad Pitagórica :

$operatorname{sen}^2 (alpha) + cos^2 (alpha) = 1$

Algunas identidades trigonométricas importantes son las siguientes:

sen (90 – α) = cos α

cos (90 – α) = sen α

sen (180 – α) = sen α

cos (180 – α) = –cos α

sen 2α = 2 sen α cos α

cos 2α = cos²α - sen²α

sen (α ± β) = sen α cos β ± cos α sen β

cos (α ± β) = cos α cos β ∓ sen α sen β

2 sen α cos β = sen (α + β) + sen (α – β);

2 sen²(α) = 1 – cos(2α);

2 cos²(α) = 1 + cos(2α);

sen α cosα + sen β cos β = sen(α + β)Cos(α - β)

FUNCION TANGENTE

En un triángulo rectángulo, la tangente (abreviada como tan o tg) es la razón entre el cateto opuesto y el cateto adyacente.

$tan(a) = BC / AC = operatorname{sen}(a) / cos(a)$

El valor de la tangente para algunos ángulos importantes es:

tan = AC / OA = BD / OB = sen / cos

tan (π/2) = tan (90°) = +∞

tan (-π/2) = tan (-90°) = -∞

tan (0) = 0

tan (π/4) = tan (45°) = 1

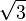
tan (π/3) = tan (60°)= $sqrt 3$

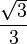
tan (π/6) = tan (30°) = $frac{sqrt{3}}{3}$

Una identidad de importancia con la tangente es:

$tan(alpha + beta) = frac {tan(alpha) + tan (beta)} {1 - tan(alpha) tan(beta)}$

SENO Y COSENO, FUNCIONES COMPLEJAS

El seno y coseno se define en matemática compleja , gracias a la fórmula de Euler como:

$cos(alpha)= frac {e^{ialpha}+e^{-ialpha}}{2}$

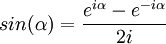
$sin(alpha)= frac {e^{ialpha}-e^{-ialpha}}{2i}$

Siendo 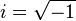$i=sqrt{-1}$ (representado también frecuentemente como j)

ANGULO

Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Otra concepción de ángulo dice que éste es la figura formada por dos rayos con origen común. Con cualquiera de estos dos conceptos, un ángulo determina una superficie abierta (subconjunto abierto de puntos del plano), al estar definido por dos semirrectas, la medida de ángulos es la medida de la abertura de estas semirrectas, que se denomina medida del ángulo.

Ángulo agudo

Es el ángulo formado por la union de dos lineas rectas en una abertura mayor de 0º y menor de 90º. A la union se le llama vertice.

Ángulo recto [

Un ángulo recto es igual a 90º, o 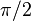$pi /2 ,$ Rad.).

Los dos lados de un ángulo recto son perpendiculares entre sí, la proyección ortogonal de uno sobre otro es un punto, que coincide con su punto de intersección.

Ángulo obtuso

Un ángulo obtuso es superior a 90º e inferior a 180º, esto es entre 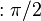$: pi /2 ,$ y $pi ,$ Rad.).

Ángulo llano

Un ángulo llano o plano es igual a 180º, o $pi ,$ Rad.).

Un ángulo de 180º.

En un ángulo llano los dos lados están alineados uno a continuación de otro dividiendo el plano en dos semiplanos.

Ángulo Cóncavo

Es el ángulo que mide más de 180º y menos de 360°

Ángulo perigonal o completo

Un ángulo perigonal es igual a 360º, esto es $2pi ,$ Rad.).

Este ángulo se obtiene al hacer girar la semirrecta hasta colocarla en su posición inicial.

Ángulos en espacios abstractos

Dado un espacio vectorial cuyo cuerpo es el conjunto de los números reales y en el que existe un producto escalar entre vectores, se define el ángulo formado por dos vectores no nulos por la expresión:

$cos theta_{xy} = frac{langle x, y rangle}{|x| |y|}$

Si el cociente anterior es 0, se dice que ambos vectores son ortogonales.