|
| MATEMATICAS - identidades trigonometricas
|
|
|
|
Son igualdades que involucran funciones trigonométricas, verificables para cualquier valor permisible de la variable o variables que se consideren
Relación pitagórica
|
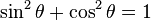
|
Identidad de la razón
|

|
estas ecuaciones de conversión pueden devolver el signo incorrecto (+ or −). Por ejemplo, si sin θ = 1/2, la conversión propuesta en la tabla indica que 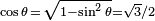 , aunque en realidad , aunque en realidad  . Para obtener la única respuesta correcta se necesitará saber en qué cuadrante está θ. . Para obtener la única respuesta correcta se necesitará saber en qué cuadrante está θ.
Función
|
sin
|
cos
|
tan
|
csc
|
sec
|
cot
|
sinθ =
|
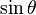
|
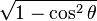
|

|

|
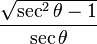
|

|
cosθ =
|

|
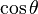
|

|
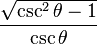
|

|

|
tanθ =
|

|

|

|

|

|
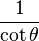
|
cscθ =
|
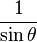
|

|

|
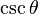
|

|

|
secθ =
|

|
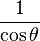
|
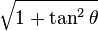
|
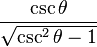
|
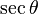
|

|
cotθ =
|
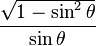
|

|

|

|

|
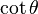
|
funciones trigonométricas
-

-
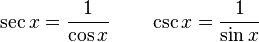
Son más difíciles de probar en la circunferencia trigonométrica o goniométrica (tiene radio=1):
-

-

-

-

Es llamada identidad trigonométrica fundamental, y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).
Por ejemplo, si se divide ambos miembros por cos², se tiene:
Calculando la recíproca de la expresión anterior:
-

Entonces puede expresarse la función seno según alguna otra conocida:
-

-

-
Teoremas de la suma y diferencia de ángulos
Pueden demostrarse según la Fórmula de Euler o mediante la proyección de ángulos consecutivos. La identidad de la tangente surge del cociente entre coseno y seno, y las restantes de la recíproca correspondiente.
-

-

-

De lo que se sigue para determinados ángulos suplementarios:
-

-

-

-

Para ángulos complementarios:
-

-

-

-

-

-

|
| Hoy habia 1 visitantes (9 clics a subpáginas) ¡Aqui en esta página!
|
|
|
|