MATEMATICAS - razones trigonometricas

MATEMATICAS - razones trigonometricas

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo $alpha ,$ , correspondiente al vértice A, situado en el centro de la circunferencia

El seno (abreviado como sen, o sin por llamarse "sinus" en latín) es la razón entre el cateto opuesto y la hipotenusa,

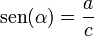
$operatorname{sen}(alpha)= frac{a}{c}$

El coseno (abreviado como cos) es la razón entre el cateto adyacente y la hipotenusa,

$cos(alpha)= frac{b}{c}$

La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto y el adyacente,

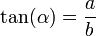
$tan(alpha)= frac{a}{b}$

Se definen la cosecante, la secante y la cotangente, como las razones recíprocas al seno, coseno y tangente, del siguiente modo:

secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:

$sec (alpha) = frac{1}{cos (alpha)} = frac{c}{b}$

cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:

$csc (alpha) = frac{1}{operatorname{sen} (alpha)} = frac{c}{a}$

cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:

$cot (alpha) = frac{1}{tan (alpha)} = frac{b}{a}$

Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés especifico en hablar de ellos o las expresiones matemáticas se simplifiquen muchísimo, los términos cosecante, secante y cotangente no suelen utilizarse.

Valor de las funciones trigonométricas

A continuación algunos valores de las funciones que es conveniente recordar:

Radián	Ángulo	sen	cos	tan	csc	sec	ctg
$0 ;$	$0^o ,$	$frac{sqrt{0}}{2}=0$	$frac{sqrt{4}}{2}=1$	$0 ,$	$infty$	$1 ,$	$infty$
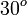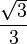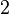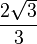$frac{pi}{6}$	$30^o ,$	$frac{sqrt{1}}{2}=frac{1}{2}$	$frac{sqrt{3}}{2}$	$frac{sqrt{3}}{3}$	$2 ,$	$frac{2sqrt{3}}{3}$	$sqrt{3}$
$frac{pi}{4}$	$45^o ,$	$frac{sqrt{2}}{2}$	$frac{sqrt{2}}{2}$	$1 ,$	$sqrt{2}$	$sqrt{2}$	$1 ,$
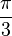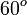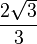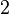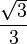$frac{pi}{3}$	$60^o ,$	$frac{sqrt{3}}{2}$	$frac{sqrt{1}}{2}=frac{1}{2}$	$sqrt{3}$	$frac{2sqrt{3}}{3}$	$2 ,$	$frac{sqrt{3}}{3}$
$frac{pi}{2}$	$90^o ,$	$frac{sqrt{4}}{2}=1$	$frac{sqrt{0}}{2}=0$	$infty$	$1 ,$	$infty$	$0 ,$

Hoy habia 10 visitantes (12 clics a subpáginas) ¡Aqui en esta página!

Este sitio web fue creado de forma gratuita con PaginaWebGratis.es. ¿Quieres también tu sitio web propio?

Registrarse gratis